Finding the Kth Largest Element in an Unsorted Array

This week, discussing about algorithms with my colleagues, one of my them came with a problem someone presented him during an interview process at some point. The problem is relatively simple to describe; given an unsorted array of elements, find the largest that occupies position k (1 ≤ k ≤ array’s length), which is also given as an input.

In other words:

Given this array [23, 1, 45, 20, 56, 75, 2, 56, 99, 53, 120] and k=2 the output should be 99.

Intuitively the solution is simple, we sort the array and we access the kth element. If we use the QuickSort algorithm the Big O notation says that we can get that with a complexity that is O(n log n) for the average case of sorting the array + O(1) for accessing the kth element. So, O(n log n) in summary.

The summary Wikipedia provides about the steps of the QuickSort algorithm is:

1. Choose a pivot in the array (an arbitrary element that use to be the one at the center of the array)
2. Partition: Move the elements with values < than the pivot before the pivot, and all elements with values > pivot after it. After this, the pivot should be in its final position.
3. Recursively apply steps 1 and 2 the subarray with smaller values and to the subarray with greater values.

Just as a reminder, the following is the basic code for the QuickSort:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
        void sort(int[] array, int firstIdx, int lastIdx) {

            int i = firstIdx;
            int j = lastIdx;

            // Determine pivot element and value (middle index element in this case)
            int pivot = array[firstIdx+(lastIdx-firstIdx)/2];

            while (i <= j) {

                // Sort in ascending order
                while (array[i] < pivot) {
                    i++;
                }
                while (array[j] > pivot) {
                    j--;
                }
                if (i <= j) {
                    swap(array, i++, j--);
                }
            }

            // Recursive calls to sort each side of the array
            if (firstIdx < j)
                sort(array, firstIdx, j);
            if (i < lastIdx)
                sort(array, i, lastIdx);
        }

    }

The time this solution takes (once the QuickSort algorithm has been adapted to order the elements in a descending order) is shown below:

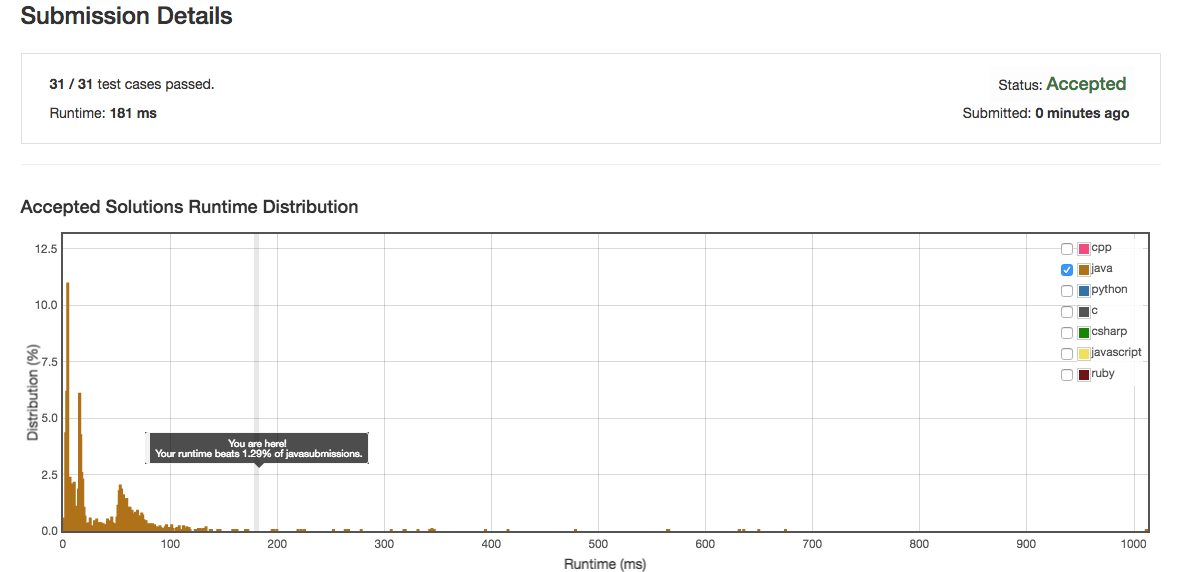
As we can see the time this solution takes is not appealing compared to other solutions in leetcode.com.

So, can we do it better? Yes! If we take advantage of the fact that after the partitioning phase, the pivot is in its final position, we can prune the quickSort avoiding one of the recursive calls, as we’re interested only in sorting the part of the array that contains the kth element.

The following code shows what I did:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
        private int prunedQuickSort(int[] array, int firstIdx, int lastIdx, int kth) {

            int i = firstIdx;
            int j = lastIdx;

            // Determine pivot element (middle index element in this case)
            int pivot;
            if (array.length == 1 || array.length % 2 == 0) {
                pivot = array[(firstIdx + (lastIdx - firstIdx) / 2)];
            } else {
                pivot = array[(firstIdx + (lastIdx - firstIdx) / 2 + 1)]; // Central element
            }

            // Scan left and right sides of the pivot and swap if necessary
            while (i <= j) {

                while (array[i] > pivot) {
                    i++;
                }

                while (array[j] < pivot) {
                    j--;
                }

                if (i <= j) {
                    swap(array, i++, j--); // Post eval increment
                }

            }

            // Recursive calls
            if (firstIdx < j && kth <= j) { // Look on the left side
                return prunedQuickSort(array, firstIdx, j, kth);
            } else {
                if (i < lastIdx && kth >= i) { // Look on the right side
                    return prunedQuickSort(array, i, lastIdx, kth);
                } else { // firstIdx == j == kth || i == lastIdx == kth <-- this is the guy
                    return array[kth];
                }
            }

        }

The main differences with the QuickSort algorithm shown above are:

1. We add a new parameter to the function arguments representingh the kth element (line 1)
2. We return the kth element value once we found it (also line 1)
3. Now we do order the array in the reverse order (line 17 and 21)
4. After the partition (lines 15-29) we’re just interested in the subarray that contains the kth position, so we prune the recursion in lines 32-40. We stop the recursion when we reach the subarray position that corresponds to the kth element, which -as it is already sorted- should contain the value we are looking for (line 38).

This time, this solution looks much better than before (181 vs 2 ms):

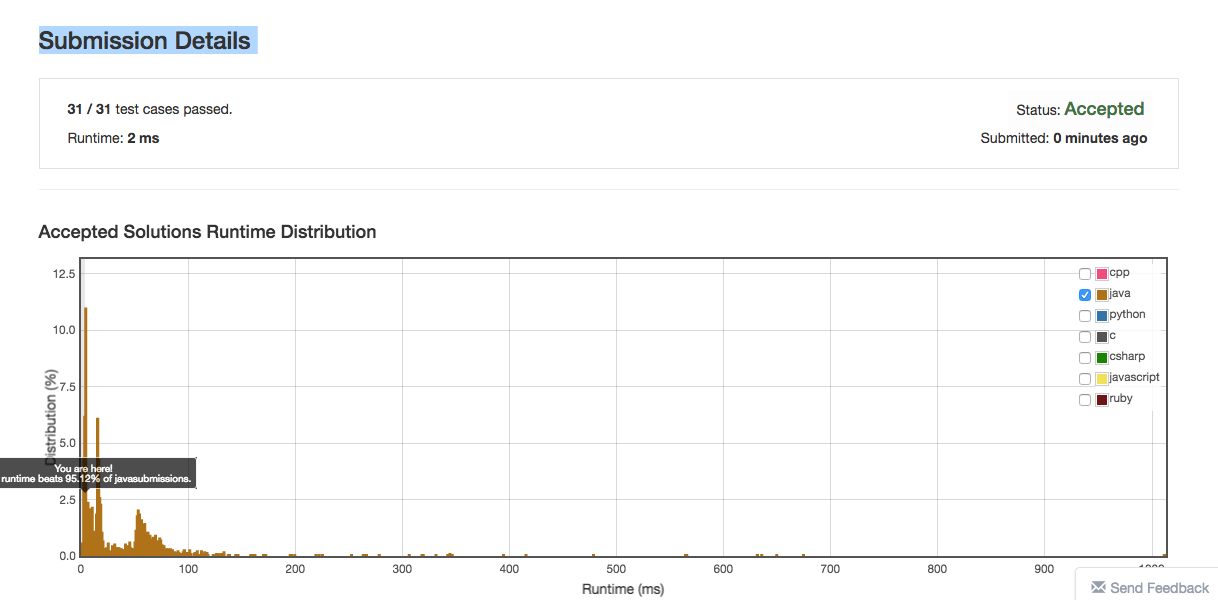
I’ve dug a little bit into the literature, and this problem is generally know as the selection algorithm. According to the Wikipedia, a selection algorithm is an algorithm for finding the kth smallest number in a list or array; such a number is called the kth order statistic. After skimming the article, it seems that the algorithm I coded corresponds to the section described as Partition-based selection and with this approach, we can get a complexity that is O(n).

You can find the complete code shown above in a Java project in here.